Introduction & Background
Overview
Welcome to Modeling with Linear & Generalized Linear Models! In this first module we will:
- Review the notation and basic statistical concepts that will recur throughout the course.
- Introduce our running motivating example: predicting house prices using regression.
By the end of this lesson you should feel comfortable with symbols like \(y\), \(\mathbf{x}\), \(\boldsymbol\beta\), and be ready to formulate and fit your first linear model.
Notation
Throughout the course we will use the following conventions:
| Symbol | Meaning |
|---|---|
| \(n\) | Number of observations (data points) |
| \(p\) | Number of predictors (features) |
| \(\mathbf{x}_i\) | The \(p\)-vector of features for observation \(i\) |
| \(y_i\) | The response (target) for observation \(i\) |
| \(\mathbf{X}\) | The \(n\times p\) design matrix whose \(i\)th row is \(\mathbf{x}_i^\top\) |
| \(\boldsymbol\beta\) | The \(p\)-vector of unknown model coefficients |
| \(\varepsilon_i\) | Random error term for observation \(i\) |
| \(\bar x\) | observed/sample means for random variables \(x\) |
| \(s^2 \) | observed/sample variance for random variables \(x\) |
Before fitting models, let’s recall some foundational ideas:
Random Variables & Expectations
- A random variable \(Y\) has a probability distribution.
- The expected value (mean) is
\[ \mathbb{E}[Y] = \mu = \int y\,dF_Y(y) \] - The variance measures spread:
\[ \mathrm{Var}(Y) = \mathbb{E}\bigl[(Y - \mu)^2\bigr] = \sigma^2. \]
Sampling & Estimation
- The sample mean of \(y_1,\dots,y_n\): \[ \bar y = \frac1n\sum_{i=1}^n y_i. \]
- The sample variance: \[ s^2 = \frac{1}{n-1}\sum_{i=1}^n (y_i - \bar y)^2. \]
Covariance & Correlation
- Covariance of two random variables \(X\) and \(Y\): \[ \mathrm{Cov}(X,Y) = \mathbb{E}\bigl[(X - \mathbb{E}[X])(Y - \mathbb{E}[Y])\bigr]. \]
- Correlation (Pearson’s \(\rho\)) is the standardized covariance: \[ \rho_{XY} = \frac{\mathrm{Cov}(X,Y)}{\sqrt{\mathrm{Var}(X)\,\mathrm{Var}(Y)}}. \]
We will see how these quantities enter into formulas for parameter estimates, tests, and confidence intervals.
Motivating Example: House Price Prediction
To ground our discussion, we’ll work throughout the course with a real-world dataset of house sales. Our goal:
Predict the sale price \(y\) of a home from features such as:
- Size (\(\text{sqft}\))
- Number of bedrooms
- Age of the home
- Neighborhood quality (that will be encoded as dummy variables)
In notation:
\[ y_i \;=\; \beta_0 + \beta_1\,\text{sqft}_i + \beta_2\,\text{beds}_i + \beta_3\,\text{age}_i + \cdots + \varepsilon_i. \]Here is a sample of 10 lines:
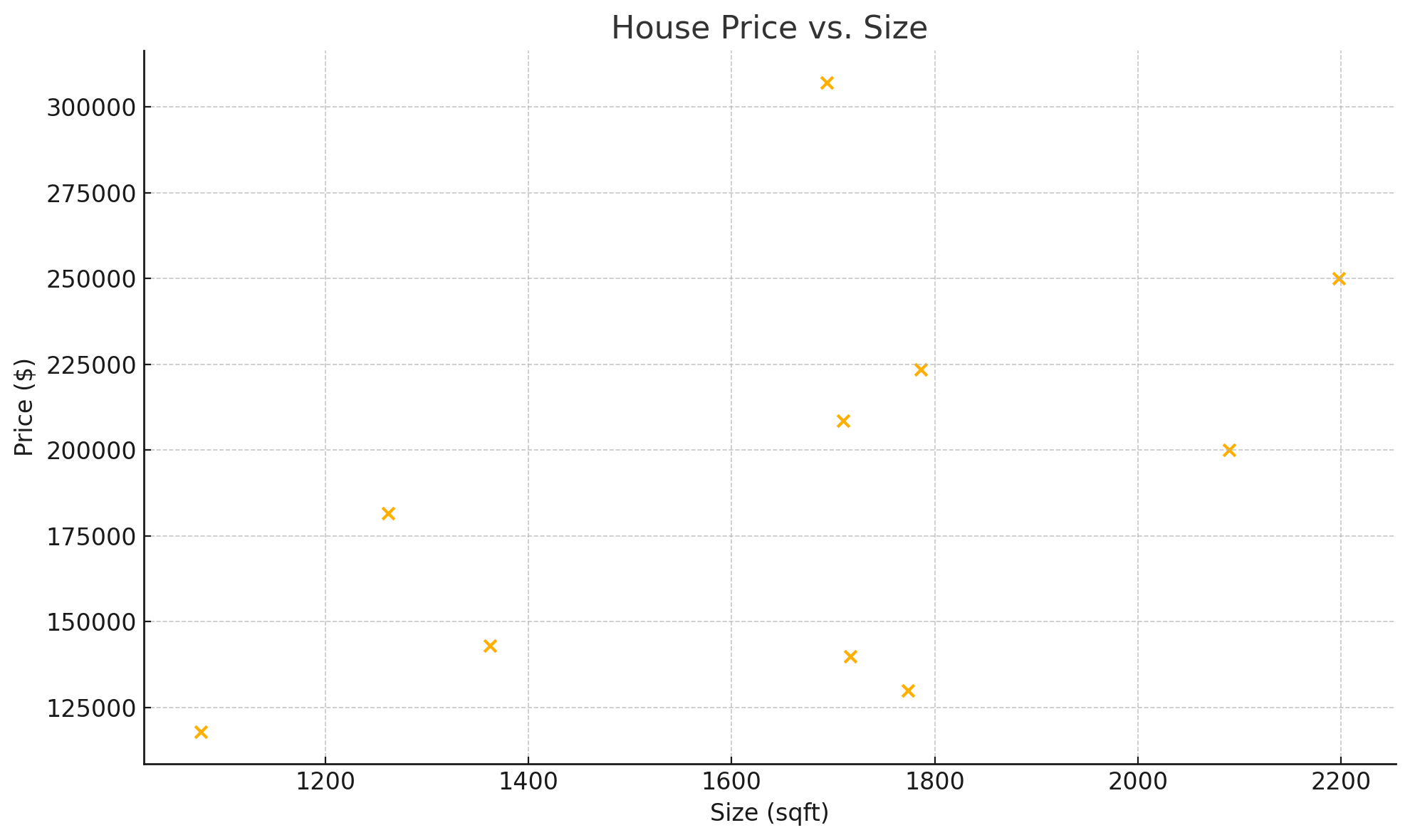
| Size | Number of bedrooms | Age | Neighborhood | Price |
|---|---|---|---|---|
| 1710 | 3 | 5 | CollgCr | 208500 |
| 1262 | 3 | 31 | Veenker | 181500 |
| 1786 | 3 | 7 | CollgCr | 223500 |
| 1717 | 3 | 91 | Crawfor | 140000 |
| 2198 | 4 | 8 | NoRidge | 250000 |
| 1362 | 1 | 16 | Mitchel | 143000 |
| 1694 | 3 | 3 | Somerst | 307000 |
| 2090 | 3 | 36 | NWAmes | 200000 |
| 1774 | 2 | 77 | OldTown | 129900 |
| 1077 | 2 | 69 | BrkSide | 118000 |
Here’s your scatter plot of Price (y) vs. Size (x):
Later modules will show how to:
- Estimate \(\boldsymbol\beta\) (Ordinary Least Squares)
- Test hypotheses about feature effects (t-tests, F-tests)
- Check model assumptions (residual diagnostics)
- Extend to generalized linear models (e.g., logistic regression)
With our notation and basic statistics clear, we’re ready to dive in to Simple Linear Regression in the next lesson!